LIMIT FUNGSI KUADRAT

LIMIT FUNGSI KUADRAT

          

            Limit biasa digunakan untuk menyatakan batas. Artinya kita boleh mendekati batas tersebut tetapi tidak boleh mencapai batas tersebut. Misalnya, kendaraan tidak dapat digunakan jika bensinnya habis. Namun kita masih bisa menggunakan kendaraan ketika bensin mendekati habis. Limit menunjukkan kecenderungan nilai suatu fungsi jika batas tertentu didekati.

1. Definisi dan Pengertian Limit

1.1. Definisi Limit

Berikut adalah definisi limit menurut Austin Louis Cauchy:

Sebuah fungsi f(x) mempunyai  jika dan hanya jika untuk sembarang bilangan real  maka terdapat bilangan real sedemikian hingga memenuhi:

 maka 

1.2. Pengertian Limit

Supaya lebih memahami pengertian limit, berikut disajikan contoh:

Perhatikan fungsi aljabar . Agar fungsi f(x) terdefinisi, nilai x dibatasi yaitu x ≠ 1. Jika batas nilai x tersebut didekati, akan diperoleh hasil bahwa nilai fungsi mendekati 3 seperti terlihat pada tabel berikut:

x	0,99	0,999	0,9999	0,99999	…	1	…	1,00001	1,0001	1,001
	2,9701	2,997001	2997	2,99997	…	-	…	3,00003	3,0003	3,003001

Pada kasus seperti di atas dikatakan limit  untuk x mendekati 1 adalah 3, ditulis: .

2. Limit Fungsi

 artinya nilai x mendekati nilai a (tetapi x ≠ a) maka f(x) mendekati nilai L.

2.1. Sifat-Sifat Teorema Limit Fungsi

1. 
2. 
3. 
4. 
5. Jika  dan  maka: 
6. 
7. 
8. , untuk 
9. Jika  maka:  untuk L ≠ 0
10. 

2.2. Menentukan Nilai dari Suatu 

1. Jika f(a) = k maka 
2. Jika  maka 
3. Jika  maka 
4. Jika  atau bentuk tertentu  maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3).
5. 
   

2.3. Limit Fungsi Tak Terhingga

1. 
2.  Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)
3.  Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x)
4.  Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x).

3. Limit Fungsi Aljabar

3.1. Limit Fungsi Aljabar Berhingga

1. Jika f(a)=C, maka nilai 
2. Jika , maka nilai 
3. Jika , maka nilai  disederhanakan dulu menjadi bentuk 1, 2, atau 3.

3.2. Limit Fungsi Aljabar Tak Terhingga

Menentukan nilai  atau :

1. Jika n = m maka 
2. Jika n > m maka 
3. Jka n < m maka 

4. Limit Fungsi Trigonometri

Untuk menghitung nilai limit fungsi trigonometri digunakan rumus-rumus berikut:

1. 
2. 
3. 
4. 

Kemudian, secara umum dapat menggunakan langkah-langkah cepat seperti di bawah ini:

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 

Jika terdapat fungsi cos maka ubahlah ke dalam bentuk sebagai berikut:

1. cos x diubah menjadi 
2.  diubah menjadi 

Berikut adalah sifat-sifat teorema limit fungsi geometri lainnya:

1. 
2. 
3. 
4. 
5. 
6. 
7. 

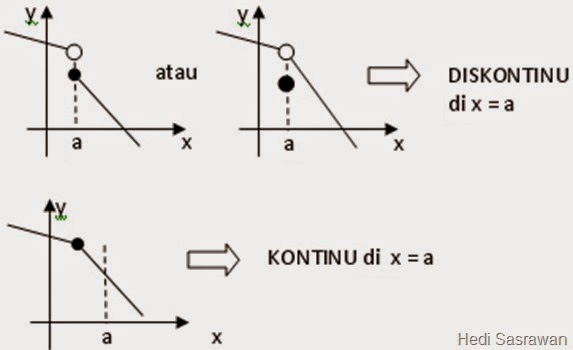
5. Kontinuitas

Suatu fungsi kontinu di x = a jika:

1. f(a) real
2. 
3. 

CONTOH SOAL

1.

  lim

x→2

 x² - 4x - 2

Pembahasan :
 

limx→2

 x² - 4x - 2 = 2² - 42 - 2 = 00 (bentuk tak tentu)

Jadi hasil faktornya adalah :

limx→2

 x² - 4x - 2 = (x-2)(x+2)(x-2) = (x+2)= (2+2) = 4

2.

limx→2

 x² - 5x + 6x² - 4

Pembahasan :

limx→2

 x² - 5x + 6x² - 4 = 2² - 5.(2) + 62² - 4 = 00 (bentuk tidak tentu)

Dengan demikian kita harus menggunakan cara lain, yaitu : dengan mengfaktorkan dan melakukan turunan. Dalam soal no.4 ini kita lakukan dengan turunan :

limx→2

 x² - 5x + 6x² - 4 = 2x - 52x = 2.(2) - 52.(2) = -14

3.

limx→∞

 4x - 12x + 1

Pembahasan:
Perhatikan pangkat tertinggi dari x pada f (x ) = 4x – 1 dan g(x) = 2x + 1. ternyata pangkat tertinggi dari x adalah satu. 

limx→∞

 4x - 12x + 1

⇔ 

limx→∞

 

4xx - 1x2xx + 1x

⇔ 

limx→∞

 

4 - 1x2 + 1x

 = 

4 - 1∞2 + 1∞

 = 

4 - 02 - 0

 = 2

4.

limx→∞

 4x + 1x² - 2

Pembahasan:
Fungsi tersebut memiliki x dengan pangkat tertinggi 2, yaitu x² yang terdapat pada x² - 2. Sehingga :

limx→∞

 4x + 1x² - 2

⇔ 

limx→∞

 

4xx² + 1x²x²x² - 2x²

⇔ 

limx→∞

 

4x + 1x²1 - 2x²

 = 

4∞ + 1(∞)²1 - 2(∞)²

 = 

0 + 01 - 0

 = 0